9718: Changing Minimum Spanning Tree
内存限制:512 MB
时间限制:4 S
题面:传统
评测方式:文本比较
上传者:
提交:2
通过:1
题目描述
An undirected graph is a graph where any edge can be traversed in both directions. A simple graph is a graph that does not have duplicate edges or self-loops. A connected graph is a graph in which there exists at least one path between any two vertices.
A spanning tree of an undirected graph is a connected subgraph that includes all the vertices of the graph and some of its edges, where there exists exactly one path between any two vertices. An undirected graph can have edge weights, and the spanning tree with the minimum sum of edge weights is called the minimum spanning tree.
Given a weighted undirected simple graph with nnn vertices and mmm edges, where the weight of each edge is required to be an integer between 111 and kkk, now we want to add one more edge under the weight constraint, such that the new graph is a simple graph that has at least one spanning tree, and the newly added edge must be included in any minimum spanning tree of it. Please help calculate how many ways to do that, and output the number of ways in modulo (109+7).
A spanning tree of an undirected graph is a connected subgraph that includes all the vertices of the graph and some of its edges, where there exists exactly one path between any two vertices. An undirected graph can have edge weights, and the spanning tree with the minimum sum of edge weights is called the minimum spanning tree.
Given a weighted undirected simple graph with nnn vertices and mmm edges, where the weight of each edge is required to be an integer between 111 and kkk, now we want to add one more edge under the weight constraint, such that the new graph is a simple graph that has at least one spanning tree, and the newly added edge must be included in any minimum spanning tree of it. Please help calculate how many ways to do that, and output the number of ways in modulo (109+7).
输入格式
The first line contains an integer TTT (1<=T<=105), indicating the number of test cases.
Then follow TTT test cases. For each test case:
The first line contains three integers nnn, mmm and kkk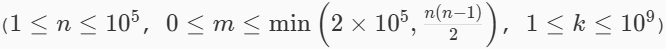 .
.
The next mmm lines describe the given simple graph. Each line of them contains three integers uuu, vvv, and www (1≤u,v≤n1 \leq u, v \leq n1≤u,v≤n, u≠vu \neq vu=v, 1≤w≤k1 \leq w \leq k1≤w≤k), representing an edge of weight www connecting uuu and vvv.
It is guaranteed that the sum of NNN and the sum of MMM over TTT test cases do not exceed 5*105 and 106, respectively.
Then follow TTT test cases. For each test case:
The first line contains three integers nnn, mmm and kkk
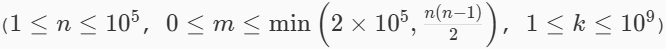 .
.The next mmm lines describe the given simple graph. Each line of them contains three integers uuu, vvv, and www (1≤u,v≤n1 \leq u, v \leq n1≤u,v≤n, u≠vu \neq vu=v, 1≤w≤k1 \leq w \leq k1≤w≤k), representing an edge of weight www connecting uuu and vvv.
It is guaranteed that the sum of NNN and the sum of MMM over TTT test cases do not exceed 5*105 and 106, respectively.
输出格式
For each test case, output an integer in one line, representing the number of ways, in modulo (109+7), to add an edge meeting the requirements.
输入样例 复制
5
3 2 2
1 2 1
2 3 2
3 3 5
1 2 3
2 3 4
1 3 5
2 1 3
1 2 3
6 6 5
1 2 3
1 3 1
2 4 2
3 5 2
2 6 4
5 6 5
2 0 25输出样例 复制
1
0
0
20
25