9676: Matrix Lottery
内存限制:512 MB
时间限制:4 S
题面:传统
评测方式:文本比较
上传者:
提交:2
通过:1
题目描述
There is a lottery box, and the lottery action corresponds to an n×nn \times nn×n matrix. Each cell in the matrix has a light bulb, which is initially turned off. Each time a lottery is drawn, a specific light bulb will be attempted to be turned on, each with a fixed probability, even if the light bulb is already on. Once a light bulb is turned on, it will remain on. In other words, each time a lottery is drawn, there is a probability of pi,jp_{i, j}pi,j of selecting the light bulb in the iii-th row and jjj-th column, or indexed (i,j)(i, j)(i,j), and attempting to turn it on (1≤i,j≤n1 \leq i, j \leq n1≤i,j≤n). If the light is already on, this operation is ignored.

Whenever all the light bulbs in a particular row, column, or diagonal are turned on, the organizer will give the player a special gift corresponding to that line. There are (2n+2)(2 n + 2)(2n+2) types of gifts, numbered from 000 to (2n+1)(2 n + 1)(2n+1), each type of gift corresponds to exactly one of the aforementioned lines, and each line corresponds to exactly one type of the gifts.

Players have a special fondness for certain gifts and are eager to know the expected number of lottery draws needed to obtain these gifts, so they come to you. You need to answer qqq queries, where the iii-th query corresponds to a number tit_iti (0<ti<22n+20 < t_i < 2^{2 n + 2}0<ti<22n+2). Let the binary representation of tit_iti in length (2n+2)(2 n + 2)(2n+2) be (b2n+1b2n⋯b0)2(b_{2 n + 1} b_{2 n} \cdots b_0)_2(b2n+1b2n⋯b0)2 such that 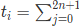
 and bj∈{0,1}b_j \in \{0, 1\}bj∈{0,1}. If bj=1b_j = 1bj=1, it indicates that the query requires obtaining the gift jjj, and you need to calculate the expected number of lottery draws with respect to these gifts, in modulo (109+7) (for more details, check the output format).
and bj∈{0,1}b_j \in \{0, 1\}bj∈{0,1}. If bj=1b_j = 1bj=1, it indicates that the query requires obtaining the gift jjj, and you need to calculate the expected number of lottery draws with respect to these gifts, in modulo (109+7) (for more details, check the output format).
输入格式
The first line contains an integer TTT (1≤T≤2001 \leq T \leq 2001≤T≤200), indicating the number of test cases.
Then follow TTT test cases. For each test case:
The first line contains two integers nnn and qqq (2≤n≤72 \leq n \leq 72≤n≤7, 1<=q<=105).
The next nnn lines describe the probabilities of selecting each cell. The iii-th line contains nnn integers wi,1,wi,2,…,wi,nw_{i, 1}, w_{i, 2}, \ldots, w_{i, n}wi,1,wi,2,…,wi,n, representing that pi,j=wi,jWp_{i, j} = \frac{w_{i, j}}{W}pi,j=Wwi,j, where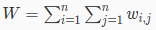
 .
.
The next (2n+2)(2 n + 2)(2n+2) lines describe the line with respect to the gifts. The iii-th line contains 2n2 n2n integers xi,1,yi,1,xi,2,yi,2,…,xi,n,yi,nx_{i, 1}, y_{i, 1}, x_{i, 2}, y_{i, 2}, \ldots, x_{i, n}, y_{i, n}xi,1,yi,1,xi,2,yi,2,…,xi,n,yi,n, representing that there are exactly nnn distinct cells with indices (xi,1,yi,1),(xi,2,yi,2),…,(xi,n,yi,n)(x_{i, 1}, y_{i, 1}), (x_{i, 2}, y_{i, 2}), \ldots, (x_{i, n}, y_{i, n})(xi,1,yi,1),(xi,2,yi,2),…,(xi,n,yi,n) lying on the line with respect to the gift (i−1)(i - 1)(i−1). It is guaranteed that all possible lines (i.e. nnn rows, nnn columns and 222 diagonals) are given.
The next line contains qqq integers t1,t2,…,tqt_1, t_2, \ldots, t_qt1,t2,…,tq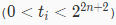 .
.
It is guaranteed that the number of test cases for n=4,5,6,7n = 4, 5, 6, 7n=4,5,6,7 does not exceed 50,10,3,150, 10, 3, 150,10,3,1 respectively.
It is also guaranteed that the sum of qqq over TTT test cases does not exceed 5*105.
Then follow TTT test cases. For each test case:
The first line contains two integers nnn and qqq (2≤n≤72 \leq n \leq 72≤n≤7, 1<=q<=105).
The next nnn lines describe the probabilities of selecting each cell. The iii-th line contains nnn integers wi,1,wi,2,…,wi,nw_{i, 1}, w_{i, 2}, \ldots, w_{i, n}wi,1,wi,2,…,wi,n, representing that pi,j=wi,jWp_{i, j} = \frac{w_{i, j}}{W}pi,j=Wwi,j, where
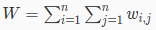
 .
.The next (2n+2)(2 n + 2)(2n+2) lines describe the line with respect to the gifts. The iii-th line contains 2n2 n2n integers xi,1,yi,1,xi,2,yi,2,…,xi,n,yi,nx_{i, 1}, y_{i, 1}, x_{i, 2}, y_{i, 2}, \ldots, x_{i, n}, y_{i, n}xi,1,yi,1,xi,2,yi,2,…,xi,n,yi,n, representing that there are exactly nnn distinct cells with indices (xi,1,yi,1),(xi,2,yi,2),…,(xi,n,yi,n)(x_{i, 1}, y_{i, 1}), (x_{i, 2}, y_{i, 2}), \ldots, (x_{i, n}, y_{i, n})(xi,1,yi,1),(xi,2,yi,2),…,(xi,n,yi,n) lying on the line with respect to the gift (i−1)(i - 1)(i−1). It is guaranteed that all possible lines (i.e. nnn rows, nnn columns and 222 diagonals) are given.
The next line contains qqq integers t1,t2,…,tqt_1, t_2, \ldots, t_qt1,t2,…,tq
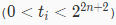 .
.It is guaranteed that the number of test cases for n=4,5,6,7n = 4, 5, 6, 7n=4,5,6,7 does not exceed 50,10,3,150, 10, 3, 150,10,3,1 respectively.
It is also guaranteed that the sum of qqq over TTT test cases does not exceed 5*105.
输出格式
For each test case, output qqq lines, the iii-th line of which contains an integer, representing your answer to the iii-th query.
It can be proved that the expected value is always a rational number. Additionally, under the constraints of this problem, it can also be proved that when that value is represented as an irreducible fraction u/du / du/d, we have . Thus, there is a unique integer fff (0<=f<109+7) such that
. Thus, there is a unique integer fff (0<=f<109+7) such that 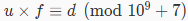 . This fff is what we need.
. This fff is what we need.
It can be proved that the expected value is always a rational number. Additionally, under the constraints of this problem, it can also be proved that when that value is represented as an irreducible fraction u/du / du/d, we have
 . Thus, there is a unique integer fff (0<=f<109+7) such that
. Thus, there is a unique integer fff (0<=f<109+7) such that 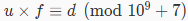 . This fff is what we need.
. This fff is what we need.输入样例 复制
1
2 12
10 20
30 40
1 1 2 2
1 2 2 1
1 1 1 2
2 1 2 2
1 1 2 1
1 2 2 2
1 2 3 4 5 6 8 9 10 16 32 63输出样例 复制
500000014
333333342
361111126
666666683
928571447
166666680
404761912
154761917
849206362
833333350
833333345
361111126