P5730 - 升级阵列

内存限制：256 MB 时间限制：2 S

题面：传统评测方式：文本比较上传者：

提交：6 通过：5

You have an array of positive integers a[1], a[2], ..., a[n] and a set of bad prime numbers b1, b2, ..., bm. The prime numbers that do not occur in the set b are considered good. The beauty of array a is the sum 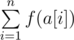$\text{[math]}$ , where function f(s) is determined as follows:

f(1) = 0;
Let's assume that p is the minimum prime divisor of s. If p is a good prime, then 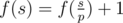$\text{[math]}$ , otherwise $\text{[math]}$ .

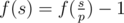You are allowed to perform an arbitrary (probably zero) number of operations to improve array a. The operation of improvement is the following sequence of actions:

Choose some number r (1 ≤ r ≤ n) and calculate the value g = GCD(a[1], a[2], ..., a[r]).
Apply the assignments: $\text{[math]}$ , $\text{[math]}$ , ..., $\text{[math]}$ .

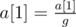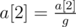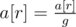What is the maximum beauty of the array you can get?

The first line contains two integers n and m (1 ≤ n, m ≤ 5000) showing how many numbers are in the array and how many bad prime numbers there are.

The second line contains n space-separated integers a[1], a[2], ..., a[n] (1 ≤ a[i] ≤ 109) — array a. The third line contains m space-separated integers b1, b2, ..., bm (2 ≤ b1 < b2 < ... < bm ≤ 109) — the set of bad prime numbers.

Print a single integer — the answer to the problem.

5 2
4 20 34 10 10
2 5

-2

Note that the answer to the problem can be negative.

The GCD(x1, x2, ..., xk) is the maximum positive integer that divides each xi.

402D 1800

5730: 升级阵列

题目描述

输入格式

输出格式

输入样例复制

输出样例复制

数据范围与提示

分类标签